2変数関数f(x,y)の(全)微分可能性、接平面
2016/10/12
問題
関数が点(1,2)で(全)微分可能かどうかを調べ、点(1,2)での接平面を求めよ。
解答の方針
以下、(a,b)を接平面と二変数関数f(x,y)の接点(今回の場合(1,2))とします。
接平面は「f(x,y)が(a,b)で全微分可能なとき」のみ存在するのですが、このような問題では全微分の可能性を調べる前に接平面の存在を仮定して計算してしまいます。
接平面をzとすると、公式
で計算することができます。
(表記 については「偏微分について」のページをご覧ください。)
その後、f(x,y)が全微分可能かどうかを調べます。
f(x,y)が(a,b)で全微分可能であることは以下のように表されます。
としたとき
この式については下記の補足を参照。
解答
接平面
が(1,2)で接平面をもつとすると、接平面の方程式より
全微分は可能か
とすると
(あとで(1,2)を代入した際に答えが0になるように調整)
(分母が0にならないようはさみうちの原理を利用)
よって
したがって点(1,2)で全微分可能で、点(1,2)での接平面の方程式は
すなわち z=4x+y-4
解説・補足
この問題では(a,b)での全微分が可能でしたが、不可能であれば当然接平面を持ちません。
また「f(x,y)が(a,b)で全微分可能であること」の厳密な定義は
f(x,y)のみに関係する定数A,Bが存在して
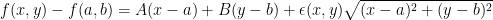
とすると
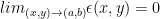 となる場合
となる場合
とすると
ですので、今回の解答だけでは不十分とされる場合があります。
必要な場合は上記の厳密な定義から今回用いた式を出しましょう。
また、何故上記のような式が出せるかについては教科書を参照してください。